区别：
1、数值不同E（X）=E（X），而E（X^2）=D（X）+E（X）*E（X）。
2、代表的意义不同，E（X）表示X的期望，而E（X^2）表示的是X^2的期望。
3、对于连续型随机变量求解的方法不同：E（X^2）的求解为x^2乘以密度函数求积分，E（X）的求解为x乘以概率密度然后求积分。对于离散型随机变量都是按照期望的定义求解：由随机变量X的分布列确定随机变量x^2的分布列后根据期望定义求解。
比如：E(X)是X的期望值，如果X等概率地取0，1，2，3，4，那么E(X)=（0+1+2+3+4）/5=2
E(X^2)是x^2的期望值，如果X等概率地取0，1，2，3，4，那么E(X^2)=（0^2+1^2+2^2+3^2+4^2)/5=6
如果是求E((X-2)^2)的话，概率还是五分之一，E((X-2)^2)=((0-2)^2+(1-2)^2+(2-2)^2+(3-2)^2+(4-2)^2)/5，
你只要把E( )这个括号里的表达式看成一个整体（如令为Y），再求出Y取每一个值的概率，剩下的就和E(X)类似了。要注意的是和每一个X对应的Y的概率可能和X不一样，比如说：
E(|X-2|)，X还是等概率地取0，1，2，3，4，那么Y=|X-2|可以取0，1，2（只有三个），其概率分别为1/5,2/5,2/5，就不是原来的等概率了。其结果为：
E(|X-2|)=E(Y)=0*(1/5)+1*(2/5)+2*(2/5)=6/5
注：这个式子也可以这么得出结果：
E(|X-2|)=（2+1+0+1+2）/5=6/5
这两种方法本质一样，但是对于复杂的情况以及理论分析（如果你以后会遇到的话），主要都是用第一种方法
扩展资料：期望的性质：
设C为一个常数，X和Y是两个随机变量。以下是数学期望的重要性质：
1、E（C）=C。
2、E（CX）=CE（X）。
3、E（X+Y）=E（X）+E（Y）。
4、当X和Y相互独立时，E（XY）=E（X）*E（Y）。
性质3和性质4可以推到到任意有限个相互独立的随机变量之和或之积的情况。
由数学期望的性质得：
当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；
当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。
设X,Y是随机变量，现在求 E(X2) 或者 E(XY) ，这两个期望的计算估计要难倒一大批的人，下面就介绍计算方法。
方法1:根据“期望”的定义来求，这是最通用也是最有效的方法。这个方法的唯一要求就是你要知道“概率 质量/密度 函数”，如果不知道那就不能用了。
方法2: 这是一个有时候非常讨巧的一个方法，很实用。
方差方差D(X)=E(X2)−[E(X)]2 ,所以只要知道 X 的方差和期望，则可以算 E(X2)。
COV(X,Y)=E[(X-EX)(Y-EY)]=E(XY)-EX*EY（这个公式非常有用，建议大家牢牢记住）。
那么E(XY)=COV(X,Y)+EX*EY
如果 EX,EY,COV(X,Y)都已知，则E(XY) 就可以算。
如果 X，Y非线性相关或相互独立，则COV(X,Y)=0，就能得到 E(XY)=E(X)E(Y)。
协方差 的补充内容
协方差与方差之间有如下关系：
D(X+Y)=D(X)+D(Y)+2Cov(X，Y)
D(X-Y)=D(X)+D(Y)-2Cov(X，Y)
协方差的性质：
1. Cov(X,Y)=Cov(Y,X)；
2. Cov(aX,bY)=abCov(X,Y)，（a，b是常数）；
3. Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2，Y)。
已知离散随机变量X的分布列为
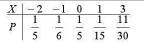
试求Y=X2与Z=|X|的分布列，
